MCR has a diverse range of projects that focus on the physiology and population dynamics of corals and organisms with which they interact, on ecosystem processes on and near coral reefs, and on the physical environment. We are developing a unified body of theory and a suite of models that can support individual projects and (more importantly) contribute to synthesis. Our two main ocean models consist of Circulation Models and Population and Community Models.
Circulation Models
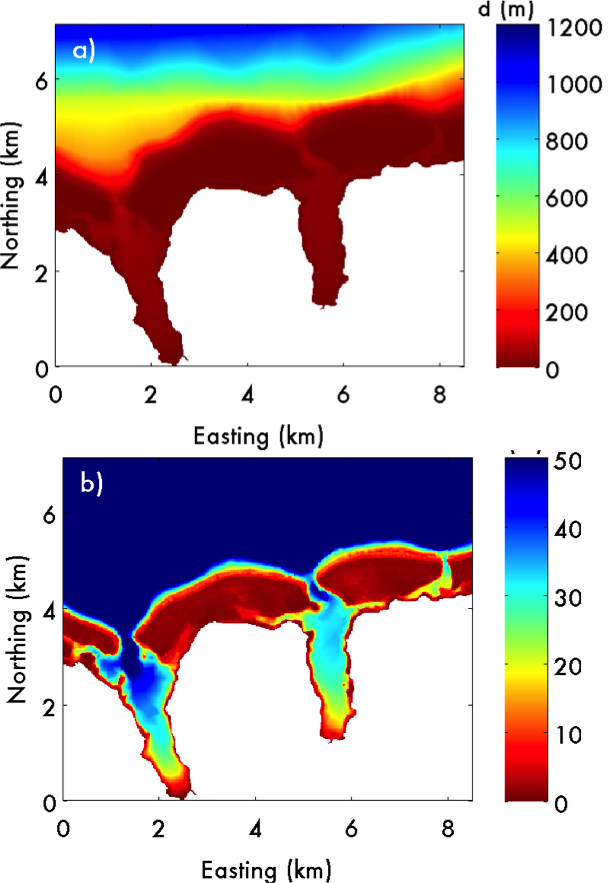
Lagoon & Island Circulation Patterns Model
- Jim Hench, Duke University
- Libe Washburn, UCSB
- Jim Leichter, Scripps Institute of Oceanography
- Johanna Rosman, Duke University
Our nearshore circulation models for the north shore incorporate our model bathymetry (<50-m) derived from satellite imagery, which feeds into our model of significant wave heights to resolve fine-grain detail; we propose to extend these models to the whole island.
A mean counter-clockwise shelf current around Moorea has been measured in our time series. We will explore this alongshore shelf current and possible associated island eddies as potential local transport and retention features influencing larval connectivity.
Spatial variation in recruitment of juvenile coral on the fore reef may be related to these transport and retention processes and location of source populations. We will examine these aspects and also are exploring the resilience consequences.
Population and Community Models
Dynamic Energy Budget Models of Coral Growth & Performance

- Roger Nisbet, UCSB
- Erik Muller, UCSB
- Peter Edmunds, CSUN
Two of the most widely recognized threats to marine biological systems that result from increased levels of atmospheric CO2 are increased sea surface temperatures and ocean acidification (OA). A key question is how marine calcifiers, a taxiconomically diverse group including animals and algae with crucial ecological roles, are responding and will continue to respond to the inexorable changes in the inorganic carbon chemistry of our oceans. Considerable research effort has been undertaken and is currently being undertaken to determine the impact of OA on the calcification potential of marine calcifiers. The interpretation of the results from these efforts is complicated by at least two factors: the taxonomic diversity of marine calcifiers and the synergistic or antagonistic impacts of other environmental stressors and factors on calcification in these organisms. Accordingly, there is a strong need to synthesize research findings within an integrative framework. For this purpose, we are using Dynamic Energy Budget (DEB) theory. DEB theory is a general, process-based modeling framework that integrates the impact of an arbitrary number of environmental stressors and resource levels on single output variables of individual organisms, such as growth, reproduction, respiration and calcification.
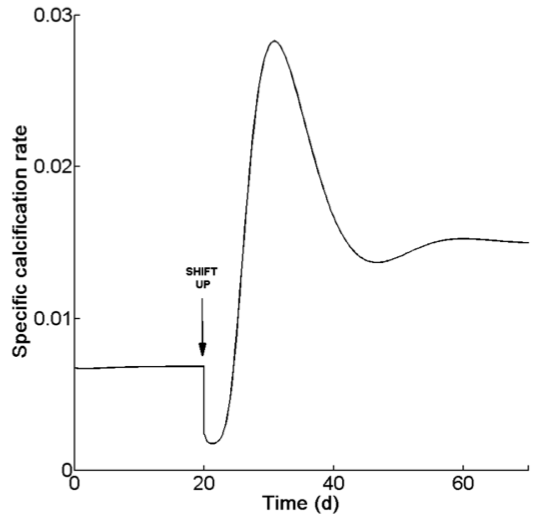 Dynamic Energy Budget (DEB) theory describes the rates at which an organism acquires resources from the environment, and subsequently utilizes the energy and nutrients therein for production and maintenance. It is a general, process-based, modular framework obeying mass and energy balances. At the core lies a set of assumptions, sometimes called ‘Standard DEB’, which specify the dynamics of mass and energy budgets in an animal. This model can be amended in order to account for organismal complexity, for instance autotrophy and multiple resource limitation. Our DEB model for syntrophic symbioses integrates a DEB theory characterization of a heterotroph with that of a photoautotroph, and serves as the basis for the research involving symbiotic interactions. This model makes realistic predictions about quantities, such as such as symbiont density, respiration and excess photosynthate production, and their trends in response to changes in irradiance and nitrogen load in corals. Furthermore, we have also developed an impact model for excess irradiance causing photoinhibition or (UV) damage and investigated this impact model in the context of coral symbioses.
Dynamic Energy Budget (DEB) theory describes the rates at which an organism acquires resources from the environment, and subsequently utilizes the energy and nutrients therein for production and maintenance. It is a general, process-based, modular framework obeying mass and energy balances. At the core lies a set of assumptions, sometimes called ‘Standard DEB’, which specify the dynamics of mass and energy budgets in an animal. This model can be amended in order to account for organismal complexity, for instance autotrophy and multiple resource limitation. Our DEB model for syntrophic symbioses integrates a DEB theory characterization of a heterotroph with that of a photoautotroph, and serves as the basis for the research involving symbiotic interactions. This model makes realistic predictions about quantities, such as such as symbiont density, respiration and excess photosynthate production, and their trends in response to changes in irradiance and nitrogen load in corals. Furthermore, we have also developed an impact model for excess irradiance causing photoinhibition or (UV) damage and investigated this impact model in the context of coral symbioses.
Giant Clam Population Projection Model
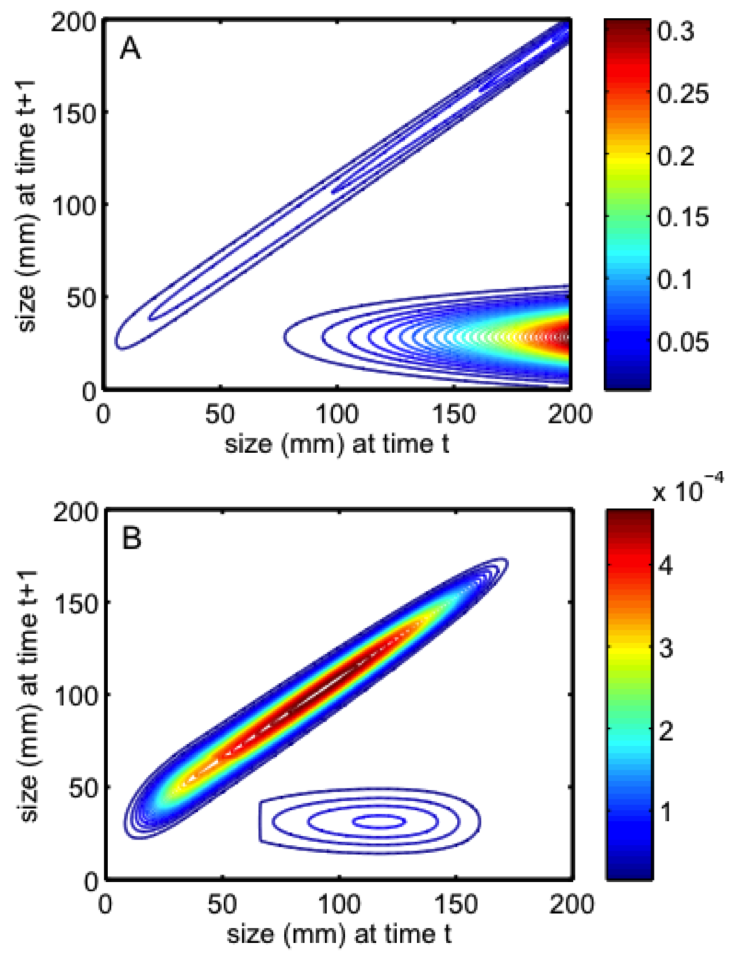 Annie Yau, UCSB
Annie Yau, UCSB- Hunter Lenihan, UCSB
We modeled a size-selective, artisanal fishery for T. maxima at a spatial scale (the island of Moorea, French Polynesia) where the amount of self-recruitment is unknown (Yau, A. PhD dissertation, 2012). We collected demographic data from 12 sites on Moorea annually from 2006-2010 to construct a size-based integral projection model (IPM) with a mix of self-recruitment and external recruitment. The IPM results indicated that in the worst xi case scenario, the population of giant clams on Moorea will exhibit a 7% decline in abundance under the present-day fishing mortality rate if it has 0% self-recruitment, but will increase exponentially if it has 100% self-recruitment. Fishing mortality decreased the projected population abundance. Finally, we evaluated the use of minimum size limits to optimize annual harvest across all possible amounts of selfrecruitment in a local population of giant clams. We used the IPM to project harvest for combinations of minimum size limit and self-recruitment ranging from 0-100% of total recruitment. A single near-optimal size limit of 135 mm resulted in maximum or near-maximum harvest across the range of self-recruitment. A single nearoptimum size limit can be applied for organisms with a variety of different life history characteristics unless a local population exhibits exponential decline. Overall, We found that the local population of giant clams on Moorea likely can support the present-day fishing mortality rate, and that size limits can optimize or nearly optimize harvest of local populations. Our work indicates that populations can be modeled and managed at the local population scale in the face of uncertainty regarding the amount of self-recruitment.
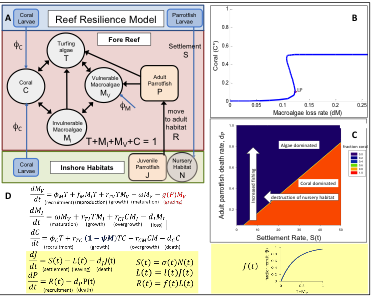 Reef Resilience Model
Reef Resilience Model
- Cherie Briggs, UCSB
- Russ Schmitt, UCSB
- Sally Holbrook, UCSB
- Tom Adam, UCSB
- Andrew Brooks, UCSB
We use two complementary modeling approaches in addition to our Leslie Matrix and Integral Projection Models to project community structure based on empirical data. Our Reef Resilience Models start with intentionally simplistic formulations (Figure at right), describing the system in broad terms, such as “coral” and “macroalgae”, to investigate the effects of general processes on the overall state of the system and then progressively build in biological details. Working towards the development of a general theory of coral reef resilience, we are developing mathematical models to investigate how all of the biological and physical processes interact to determine the resilience of the coral reef systems to various perturbations and anthropogenic stressors. Recent modeling efforts by others have used simple mathematical descriptions of the interactions between coral, macroalgae, and turf algae to investigate the processes that lead to rapid shifts from coral-dominated to algae-dominated reefs, and that prohibit the ready return to a coral-dominated state. Our model of reef resiliency will build on these earlier efforts.



